Page 22 - EngineerIT July 2022

ADVANCED FILTER TECHNOLOGY

Classical filter types with distinct insertion loss and group delay
characteristics are Butterworth, Chebyshev, Elliptic and Bessel.
Each one is usually defined by an order number that describes
how many reactive elements are in the filter. The higher the
order number, the faster the frequency roll-off.
When considering similarly ordered filters, the Butterworth
style offers a maximally flat pass-band response at the expense
of frequency roll-off, whereas a Chebyshev filter has good
frequency roll-off with some pass-band ripple. An elliptic filter
(sometimes called the Cauer-Chebyshev) has more frequency
roll-off than a Chebyshev filter, but consequently ripple in
both the pass band and the stop band. The Bessel filter has
maximally flat frequency and group delay responses, although
with the worst frequency roll-off performance. For illustrative
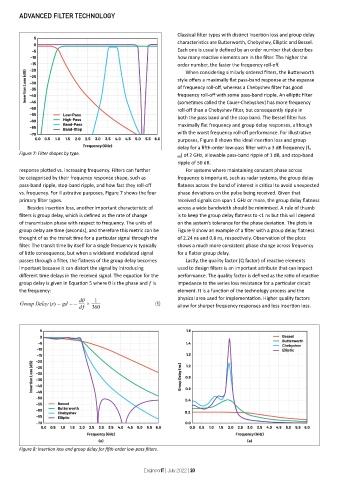
purposes, Figure 8 shows the ideal insertion loss and group
delay for a fifth-order low-pass filter with a 3 dB frequency (f 3
Figure 7: Filter shapes by type. dB) of 2 GHz, allowable pass-band ripple of 1 dB, and stop-band
ripple of 50 dB.
response plotted vs. increasing frequency. Filters can further For systems where maintaining constant phase across
be categorised by their frequency response shape, such as frequency is important, such as radar systems, the group delay
pass-band ripple, stop-band ripple, and how fast they roll-off flatness across the band of interest is critical to avoid unexpected
vs. frequency. For illustrative purposes, Figure 7 shows the four phase deviations on the pulse being received. Given that
primary filter types. received signals can span 1 GHz or more, the group delay flatness
Besides insertion loss, another important characteristic of across a wide bandwidth should be minimised. A rule of thumb
filters is group delay, which is defined as the rate of change is to keep the group delay flatness to <1 ns but this will depend
of transmission phase with respect to frequency. The units of on the system’s tolerance for the phase deviation. The plots in
group delay are time (seconds), and therefore this metric can be Figure 9 show an example of a filter with a group delay flatness
thought of as the transit time for a particular signal through the of 2.24 ns and 0.8 ns, respectively. Observation of the plots
filter. The transit time by itself for a single frequency is typically shows a much more consistent phase change across frequency
of little consequence, but when a wideband modulated signal for a flatter group delay.
passes through a filter, the flatness of the group delay becomes Lastly, the quality factor (Q factor) of reactive elements
important because it can distort the signal by introducing used to design filters is an important attribute that can impact
different time delays in the received signal. The equation for the performance. The quality factor is defined as the ratio of reactive
group delay is given in Equation 5 where θ is the phase and ƒ is impedance to the series loss resistance for a particular circuit
the frequency: element. It is a function of the technology process and the
physical area used for implementation. Higher quality factors
allow for sharper frequency responses and less insertion loss.

Figure 8: Insertion loss and group delay for fifth-order low-pass filters.

EngineerIT | July 2022 | 20