Page 23 - EngineerIT March 2022

MEASUREMENT

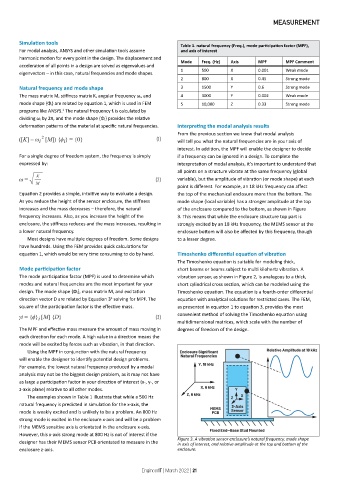
Simulation tools Table 1. natural frequency (Freq.), mode participation factor (MPF),
For modal analysis, ANSYS and other simulation tools assume and axis of interest
harmonic motion for every point in the design. The displacement and
acceleration of all points in a design are solved as eigenvalues and Mode Freq. (Hz) Axis MPF MPF Comment
eigenvectors – in this case, natural frequencies and mode shapes. 1 500 X 0.001 Weak mode
2 800 X 0.45 Strong mode
Natural frequency and mode shape 3 1500 Y 0.6 Strong mode
The mass matrix M, stiffness matrix K, angular frequency ω i, and 4 3000 Y 0.002 Weak mode
mode shape {Φ i} are related by equation 1, which is used in FEM 5 10,000 Z 0.33 Strong mode
1
programs like ANSYS. The natural frequency f i is calculated by
dividing ω i by 2π, and the mode shape {Φ i} provides the relative
deformation patterns of the material at specific natural frequencies. Interpreting the modal analysis results
From the previous section we know that modal analysis
will tell you what the natural frequencies are in your axis of
interest. In addition, the MPF will enable the designer to decide
For a single degree of freedom system, the frequency is simply if a frequency can be ignored in a design. To complete the
expressed by: interpretation of modal analysis, it’s important to understand that
all points on a structure vibrate at the same frequency (global
variable), but the amplitude of vibration (or mode shape) at each
point is different. For example, an 18 kHz frequency can affect
Equation 2 provides a simple, intuitive way to evaluate a design. the top of the mechanical enclosure more than the bottom. The
As you reduce the height of the sensor enclosure, the stiffness mode shape (local variable) has a stronger amplitude at the top
increases and the mass decreases – therefore, the natural of the enclosure compared to the bottom, as shown in Figure
frequency increases. Also, as you increase the height of the 3. This means that while the enclosure structure top part is
enclosure, the stiffness reduces and the mass increases, resulting in strongly excited by an 18 kHz frequency, the MEMS sensor at the
a lower natural frequency. enclosure bottom will also be affected by this frequency, though
Most designs have multiple degrees of freedom. Some designs to a lesser degree.
have hundreds. Using the FEM provides quick calculations for
equation 1, which would be very time consuming to do by hand. Timoshenko differential equation of vibration
The Timoshenko equation is suitable for modeling thick,
Mode participation factor short beams or beams subject to multi kilohertz vibration. A
The mode participation factor (MPF) is used to determine which vibration sensor, as shown in Figure 2, is analogous to a thick,
modes and natural frequencies are the most important for your short cylindrical cross section, which can be modeled using the
design. The mode shape {Φ i}, mass matrix M, and excitation Timoshenko equation. The equation is a fourth-order differential
1
direction vector D are related by Equation 3 solving for MPF. The equation with analytical solutions for restricted cases. The FEM,
square of the participation factor is the effective mass. as presented in equation 1 to equation 3, provides the most
convenient method of solving the Timoshenko equation using
multidimensional matrices, which scale with the number of
The MPF and effective mass measure the amount of mass moving in degrees of freedom of the design.
each direction for each mode. A high value in a direction means the
mode will be excited by forces such as vibration, in that direction.
Using the MPF in conjunction with the natural frequency
will enable the designer to identify potential design problems.
For example, the lowest natural frequency produced by a modal
analysis may not be the biggest design problem, as it may not have
as large a participation factor in your direction of interest (x-, y-, or
z-axis plane) relative to all other modes.
The examples shown in Table 1 illustrate that while a 500 Hz
natural frequency is predicted in simulation for the x-axis, the
mode is weakly excited and is unlikely to be a problem. An 800 Hz
strong mode is excited in the enclosure x-axis and will be a problem
if the MEMS sensitive axis is orientated in the enclosure x-axis.
However, this x-axis strong mode at 800 Hz is not of interest if the
designer has their MEMS sensor PCB orientated to measure in the Figure 3. A vibration sensor enclosure’s natural frequency, mode shape
in axis of interest, and relative amplitude at the top and bottom of the
enclosure z-axis. enclosure.

EngineerIT | March 2022 | 21