Page 26 - EngineerIT March 2022

MEASUREMENT

Table 4. First four significant modes for cylinder and rectangle shapes

Mode Cylinder (Hz) Rectangle (Hz)
1 11,890 5030.4
2 30,077 10,559
3 40,506 14,270
4 50,777 15,750
Bold = mode participation factor > 0.1
Not bold = 0.01 < mode participation factor < 0.1

Equation 5 is a useful tool to show the relative performance of
different geometries. Equations 4 and 5 predict four independent
solutions below the critical frequency. Table 4 summarises the
FEM results and confirms the first four significant modes.

What is the maximum recommended height for my
sensor?
Equations 4 and 5 are useful, but they do not provide analytical
guidance on the trade-off between the vertical height of the
enclosure and the first significant natural frequency possible.
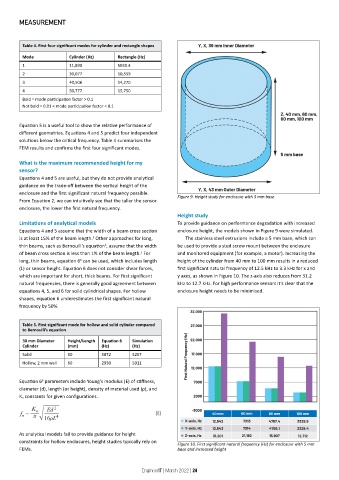
From Equation 2, we can intuitively see that the taller the sensor Figure 9. Height study for enclosure with 5 mm base
enclosure, the lower the first natural frequency.
Height study
Limitations of analytical models To provide guidance on performance degradation with increased
Equations 4 and 5 assume that the width of a beam cross section enclosure height, the models shown in Figure 9 were simulated.
is at least 15% of the beam length. Other approaches for long, The stainless steel extrusions include a 5 mm base, which can
5
thin beams, such as Bernoulli’s equation , assume that the width be used to provide a stud screw mount between the enclosure
6
of beam cross section is less than 1% of the beam length. For and monitored equipment (for example, a motor). Increasing the
5
6
long, thin beams, equation 6 can be used, which includes length height of the cylinder from 40 mm to 100 mm results in a reduced
(L) or sensor height. Equation 6 does not consider shear forces, first significant natural frequency of 12.5 kHz to 3.3 kHz for x and
which are important for short, thick beams. For first significant y axes, as shown in Figure 10. The z-axis also reduces from 31.2
natural frequencies, there is generally good agreement between kHz to 12.7 kHz. For high performance sensors it’s clear that the
equations 4, 5, and 6 for solid cylindrical shapes. For hollow enclosure height needs to be minimised.
shapes, equation 6 underestimates the first significant natural
frequency by 50%.

Table 5. First significant mode for hollow and solid cylinder compared
to Bernoulli’s equation
30 mm Diameter Height/Length Equation 6 Simulation
Cylinder (mm) (Hz) (Hz)
Solid 60 5872 5267
Hollow, 2 mm wall 60 2930 5911

Equation 6 parameters include Young’s modulus (E) of stiffness,
6
diameter (d), length (or height), density of material used (ρ), and
K n constants for given configurations.

As analytical models fail to provide guidance for height
constraints for hollow enclosures, height studies typically rely on
Figure 10. First significant natural frequency (Hz) for enclosure with 5 mm
FEMs. base and increased height

EngineerIT | March 2022 | 24